║ A Functional Block Coding Language ║ 2025 07 19 ║ Life, Coding ║ ║ <<< ║
╚════════════════════════════════════╩════════════╩══════════════╝ ╚═════╝
╔════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════╗
║ ║
║ A little over a year ago I stumbled upon "functional programming," and taught myself the basics of Haskell syntax. Having a ║
║ little bit of a background in Python at the time, learning how to write algorithms without the help of "traditional" loops or ║
║ variables, coding in Haskell proved to be a fun challenge at the time. ║
║ ║
║ Then relatively recently, I participated in a small, educational video game company's month-long internship program. As an ║
║ assignment, we were meant to design a game that would teach players the basics of astronomy, botany, chemistry, programming, ║
║ etc., etc. I chose to work with programming, and I had the idea to teach players to think and code in a functional paradigm. ║
║ ║
║ That's when, after a series of bad ideas, my idea of "LambdaBlocks" came into mind. ║
║ ║
║ *** A Series of Bad Ideas *** ║
║ My first idea was really bad. I initially decided to work on a "little alchemist" kind of game, where the player would combine ║
║ simple functions (like Haskell's "succ" or "id") to create more complicated functions. But this would completely dodge the ║
║ whole idea of teaching the basics of functional programming. It was a terrible idea. ║
║ ║
╚════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════╝
╔════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════╗
║ ║
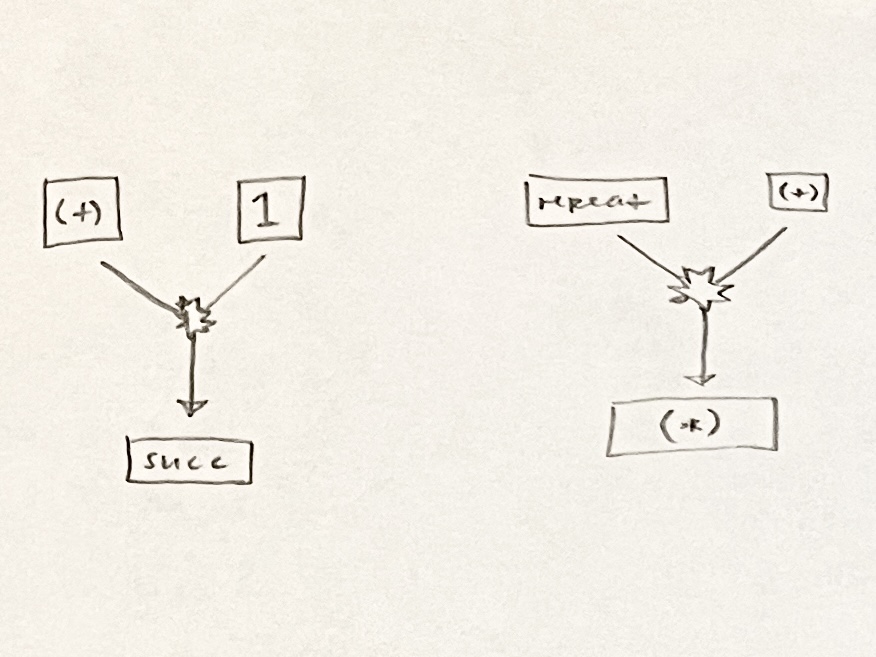
║ I then decided to create what would essentially be a block code version of lambda calculus. This was better than the previous ║
║ idea, but it still wasn't good. The company I was interning at was probably expecting a demographic of really young kids, and ║
║ throwing them into a Turing tarpit didn't sound like a very productive idea. I won't even pretend I understand lambda calculus ║
║ all that much. ║
║ ║
╚════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════╝
╔════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════╗
║ ║
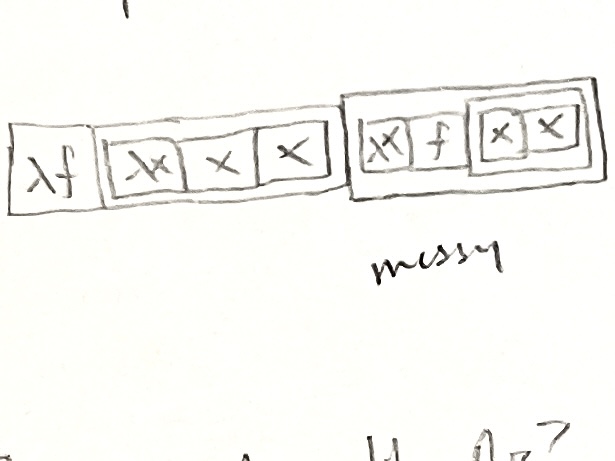
║ My third idea didn't seem all that bad. I decided to model a block coding language after Haskell. At first, the language I was ║
║ designing wouldn't be exactly like Haskell. I took the vague concept of "chaining" functions together, which would look like a ║
║ horizontal tower of many legos, and these would simplify into a single value, as elegantly as reductions of functions in ║
║ lambda calculus. ║
║ ║
║ Except it wasn't elegant. It was really, really ugly, and I hated it after a few days. I couldn't come up with an elegant ║
║ syntax (not really syntax, but a concept of how the language would work) and I felt I needed to scrap that idea after throwing ║
║ too many parentheses in (that's when it turned into Haskell, lego edition). ║
║ ║
╚════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════╝
╔════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════╗
║ ║
║ *** The Perfect Fourth Idea *** ║
║ Then, whether by some divine intervention or bad mayo in my chicken sandwich, I came up with what would have been the best ║
║ concept of a functional block coding language. Explaining it without visuals would be difficult, so I've prepared some ║
║ illustrations, along with notes from the time of designing this. ║
║ ║
╚════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════╝
╔════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════╗
║ ║
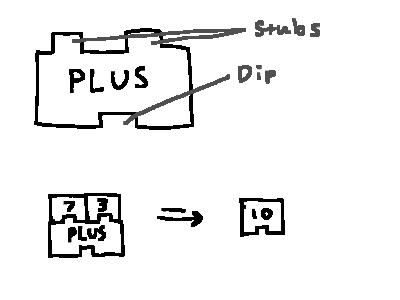
║ Functions would take the form of blocks (obviously). These blocks are composed of stubs and dips. Stubs are where other blocks ║
║ connect, and are where the function's parameters go. Every block comes with one dip, which acts like their return value. ║
║ ║
╚════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════╝
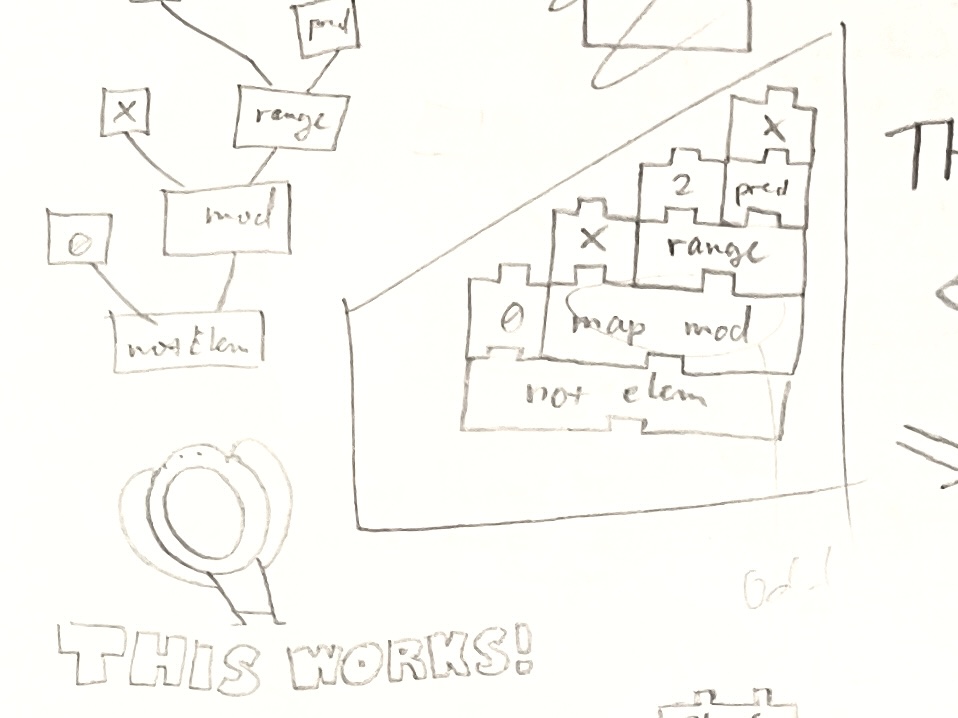
╔════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════╗
║ ║
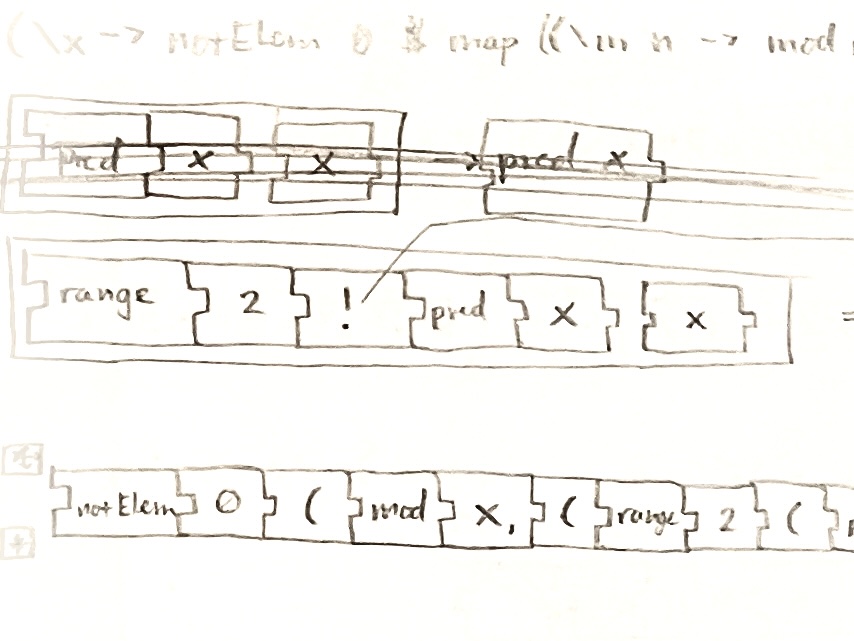
║ In this language (LambdaBlocks), groups of blocks, called stacks, can either be defined as a function or evaluated as a ║
║ literal value. The following diagram is one of an (unoptimized) example of a prime-checking function: ║
║ ║
╚════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════╝
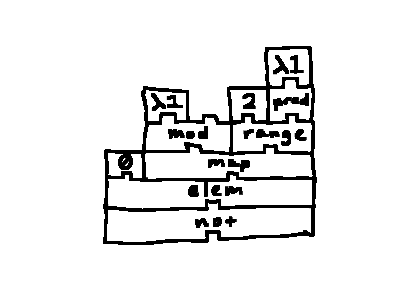
╔════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════╗
║ ║
║ Stacks aren't exactly parsed from the top to bottom. Instead, the interpreter starts at the bottom block, and checks if all ║
║ parameters are of the correct type. If so, parse the block and its parameters! If not, then continue up the stack (doing so in ║
║ a somewhat recursive fashion) until the parameters of a given block are all the correct type. ║
║ ║
╚════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════╝
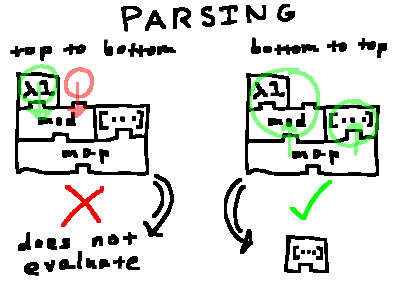
╔════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════╗
║ ║
║ This seems needlessly complicated, but it actually allows for higher order functions. The "mod" block is supposed to be passed ║
║ into the "map" block along with its parameter. However, if the interpreter parsed the stack from the top, then it would try to ║
║ evaluate the "mod" block before rightfully passing it into the "map" block, obviously introducing issues involving functions ║
║ as parameters (which is like, the whole point to functional programming!). Parsing the stack from the bottom allows for the ║
║ "mod" and its parameter to be passed into the "map" block, allowing for higher order functions to be used in function ║
║ definitions. ║
║ ║
╚════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════╝
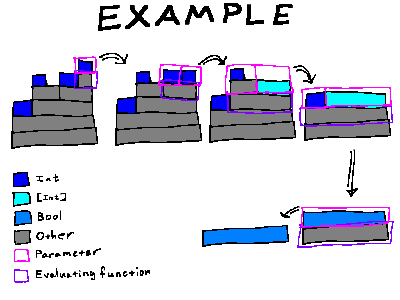
╔════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════╗
║ ║
║ There's a lot more to this language, though. I modeled it after Haskell (the prime function I drew is actually based on a ║
║ simple Haskell prime function), so there are other features I've implemented in its design, like guards and recursion. ║
║ ║
║ *** So what Happened with the Internship? *** ║
║ I was frantically putting a project together when the assignment was due in two days. I was hard-coding many different cases ║
║ that stacks may come in, knowing very well that at my level of programming experience, I would not be able to create a valid ║
║ interpreter without several more weeks. ║
║ ║
║ Then, the day before my presentation, I learned the assignment was just that. I had to present the concept of my language's ║
║ design. It turns out, creating this language was not at all a requirement. ║
║ ║
║ Maybe I would have been justified at being a little annoyed at myself, but it was never explicitly stated that I only needed ║
║ to present my concept. But out of that stressful, and pointless, work, a cool idea came out of it. ║
║ ║
╚════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════╝
